「RELION」の版間の差分
提供: Eospedia
細 |
|||
| 行6: | 行6: | ||
<math>Y</math>: 事前情報 | <math>Y</math>: 事前情報 | ||
<math>\Theta</math>：パラメータセット | <math>\Theta</math>：パラメータセット | ||
| + | |||
尤度の定義：<math>(k, \phi, \Theta(n), Y)</math> が与えられたときの画像<math>X_i</math>となるときの尤度 | 尤度の定義：<math>(k, \phi, \Theta(n), Y)</math> が与えられたときの画像<math>X_i</math>となるときの尤度 | ||
| 行11: | 行12: | ||
<math>P(X_i | k, \phi, \Theta^{(n)})=</math> | <math>P(X_i | k, \phi, \Theta^{(n)})=</math> | ||
| − | i: i番目の画像 | + | <math>i</math>: i番目の画像 <math>(n)</math>: n回目 <math>j</math>: フーリエ成分j (2次元フーリエ空間：実験画像２Ｄ） <math>J</math>: フーリエ成分の数 <math>\sigma^{2}_{i}j^{(n)}</math>: ノイズの分散（分解能毎で予測される）、データから推定 <math>\rm{CTF}_{ij}</math>: i番目の画像のフーリエ成分jのCTF（コントラスト伝達関数）の値 <math>l</math>: フーリエ成分l(３次元フーリエ空間：３Ｄマップ） <math>L</math>: フーリエ成分の数 <math>k</math>: k番目の３Ｄマップ <math>\phi</math>: 回転（３自由度）＋平行移動（２自由） |
| − | + | ||
| − | (n): n回目 | + | |
| − | + | ||
| − | j: フーリエ成分j (2次元フーリエ空間：実験画像２Ｄ） | + | |
| − | + | ||
| − | J: フーリエ成分の数 | + | |
| − | + | ||
| − | sigma^ | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | l: フーリエ成分l(３次元フーリエ空間：３Ｄマップ） | + | |
| − | + | ||
| − | L: フーリエ成分の数 | + | |
| − | + | ||
| − | k: k番目の３Ｄマップ | + | |
| − | |||
==== [[RELIONのMacへの導入]]==== | ==== [[RELIONのMacへの導入]]==== | ||
==== [[RELIONのLinuxへの導入]]==== | ==== [[RELIONのLinuxへの導入]]==== | ||
==== [[RELIONチュートリアル]]==== | ==== [[RELIONチュートリアル]]==== | ||
2017年2月16日 (木) 12:58時点における版
RELOIONのアルゴリズムに関して、整理したページになります。すこしずつまとめたいと思います。
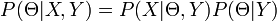
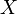: 観測されたデータ
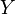: 事前情報
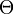：パラメータセット
尤度の定義：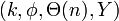
が与えられたときの画像
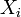となるときの尤度
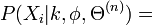
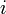: i番目の画像 
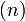: n回目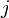 
: フーリエ成分j (2次元フーリエ空間：実験画像２Ｄ） 
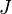: フーリエ成分の数 
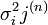: ノイズの分散（分解能毎で予測される）、データから推定 
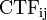: i番目の画像のフーリエ成分jのCTF（コントラスト伝達関数）の値 
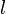: フーリエ成分l(３次元フーリエ空間：３Ｄマップ） 
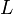: フーリエ成分の数 
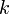: k番目の３Ｄマップ 
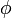: 回転（３自由度）＋平行移動（２自由）
