「主成分分析」の版間の差分
提供: Eospedia
| (2人の利用者による、間の13版が非表示) | |||
| 行1: | 行1: | ||
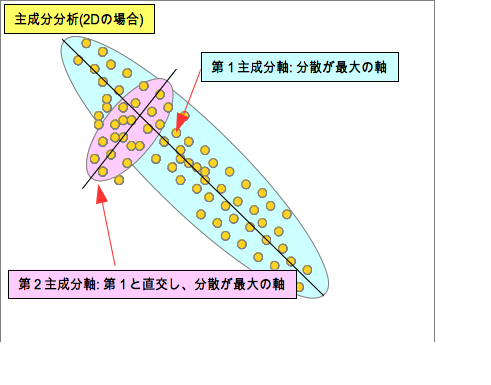
| − | '''主成分分析'''(Principal Component Analysis) | + | '''主成分分析'''(Principal Component Analysis)とは、多変量を要素としてもつベクトルデータの集合に対して、多変量空間の中で、各ベクトルデータをある軸に投影した場合に最も大きな分散をもつ軸(主軸)を求め、順次、それと直交する(無相関の)軸で、最も大きな分散を持つ軸を求めていく手法である。計算を打ち切った場合に、それ以降の情報は誤差として取り扱われる。 |
[[画像:Fig-PCA.png]] | [[画像:Fig-PCA.png]] | ||
| 行5: | 行5: | ||
== 主成分分析の実行例 == | == 主成分分析の実行例 == | ||
=== 画像毎の主成分分析 === | === 画像毎の主成分分析 === | ||
| − | <div>主に[[mrcImagePCA]] | + | <div>主に[[mrcImagePCA]]を使用して、複数画像の分類を行います。</div> |
<br> | <br> | ||
<div>[[:Media:Input-PCA.zip|入力ファイル]]の画像</div> | <div>[[:Media:Input-PCA.zip|入力ファイル]]の画像</div> | ||
<div>[[画像:Input-PCA.png]]</div> | <div>[[画像:Input-PCA.png]]</div> | ||
| − | <div> | + | <div>10通りの回転(縦)画像に10通りのノイズ(横)をそれぞれ掛けています。(計100個)</div> |
<br> | <br> | ||
| − | <div>まず、[[mrcImagePCA]] | + | <div>まず、[[mrcImagePCA]]を使用して主軸を求めます。</div> |
<br> | <br> | ||
| 行87: | 行87: | ||
<div>コマンド実行後に固有値を確認します。</div> | <div>コマンド実行後に固有値を確認します。</div> | ||
| + | <br> | ||
| + | |||
| + | <div>EIGEN_INFOのデータ</div> | ||
| + | <pre> | ||
| + | 0 485 13783745.48 16.25 | ||
| + | 1 600 6874158.21 24.36 | ||
| + | 2 997 6040647.42 31.48 | ||
| + | 3 529 5425460.64 37.88 | ||
| + | 4 834 4720681.32 43.45 | ||
| + | 5 879 3932086.98 48.08 | ||
| + | 6 842 3632776.78 52.37 | ||
| + | 7 645 3182620.81 56.12 | ||
| + | 8 566 2449230.98 59.01 | ||
| + | 9 1116 1328891.76 60.57 | ||
| + | 10 1031 1287023.24 62.09 | ||
| + | 11 579 1257054.49 63.57 | ||
| + | 12 1080 1214056.15 65.01 | ||
| + | 13 856 1161105.65 66.38 | ||
| + | 14 934 1144996.99 67.73 | ||
| + | |||
| + | -以下略- | ||
| + | |||
| + | </pre> | ||
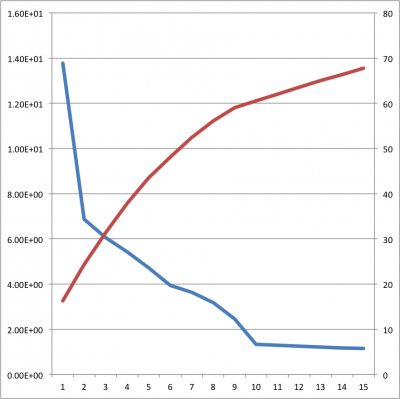
| + | <div>固有値(第3列目)が高い順にデータが並んでいます。下図をご覧下さい。今回は第8成分当たりまでの固有値が高くなっています。60%の分散まで説明できることが分かります。</div> | ||
| + | <div>[[画像:EigenValuePCA-mrcImagePCA.png|400px]]</div> | ||
| + | <br> | ||
| + | |||
| + | <div>第1 ~ 3主成分にて散布図の様子を見てみます。</div> | ||
| + | <div>[[mrcImagePCA]]のオプション-o で指定したファイルには固有値が高い順にそれぞれの画像毎のベクトル成分が格納されています。よって、このデータの上位部分を使って画像がどのグループに属しているかを見ることができます。[[mrcImageMakeDump]]を使うと、[[mrcImage]]のデータを[[ASCII]]として取り出すことができます。</div> | ||
| + | <br> | ||
| + | |||
| + | <div>[[:Media:Output-PCA.tsv.zip|各ファイルから第10成分までを取り出してまとめたデータ]]</div> | ||
| + | <pre> | ||
| + | -1002.110000 1962.390000 2375.080000 3780.900000 1531.830000 -3511.960000 -524.329000 1190.540000 -1106.170000 337.342000 | ||
| + | -1111.780000 2439.510000 2452.540000 3826.020000 1630.650000 -3519.130000 -457.767000 1531.510000 -316.514000 -2399.750000 | ||
| + | -844.584000 2207.500000 2577.200000 3895.480000 1722.810000 -3401.740000 -573.914000 961.414000 -1120.780000 75.002400 | ||
| + | -897.296000 2107.620000 2308.710000 3974.960000 1590.460000 -3559.020000 -836.757000 1690.460000 -332.499000 46.332400 | ||
| + | -639.501000 2286.200000 2513.990000 3868.320000 1741.350000 -3316.310000 -553.213000 1443.870000 -1044.260000 560.677000 | ||
| + | -1015.980000 2549.020000 2049.920000 3854.560000 1503.460000 -3118.820000 -919.956000 1212.420000 -792.175000 1047.500000 | ||
| + | -892.673000 2168.280000 2455.920000 3951.430000 1400.510000 -3498.790000 -528.413000 1509.180000 -1141.580000 10.826800 | ||
| + | -799.775000 2190.870000 2994.040000 3730.140000 1208.160000 -3002.190000 -538.733000 800.946000 -1115.250000 380.240000 | ||
| + | -1061.460000 2100.710000 2348.670000 3881.800000 1573.210000 -3440.970000 -606.476000 1363.520000 -649.180000 422.532000 | ||
| + | -782.003000 2198.650000 2594.880000 3976.130000 1891.720000 -3371.260000 -531.849000 1410.830000 -957.755000 148.813000 | ||
| + | -4295.390000 4650.010000 2406.060000 -2699.870000 1602.340000 2108.780000 1198.180000 -963.790000 565.743000 256.211000 | ||
| + | -4371.810000 4724.700000 2581.440000 -2274.290000 1625.690000 1392.540000 1677.500000 -492.734000 770.713000 -2612.010000 | ||
| + | |||
| + | -中略- | ||
| + | |||
| + | 533.205000 -1655.000000 3206.460000 1451.350000 -4268.840000 -120.817000 900.958000 -2478.230000 428.414000 361.083000 | ||
| + | 667.314000 -1569.670000 2828.330000 1229.300000 -4102.610000 -108.603000 1067.760000 -2409.760000 875.312000 -147.388000 | ||
| + | 703.368000 -1789.180000 3114.700000 1694.560000 -4408.100000 -286.116000 1112.690000 -2717.040000 595.316000 -136.777000 | ||
| + | 546.967000 -2147.200000 3076.260000 1691.570000 -4386.750000 -567.557000 963.625000 -2624.400000 913.221000 -49.355200 | ||
| + | 567.210000 -1505.020000 2555.640000 1290.990000 -4242.580000 -407.482000 1022.360000 -2779.230000 636.427000 308.664000 | ||
| + | 727.232000 -1522.510000 2804.310000 1861.250000 -4377.870000 -163.006000 1417.020000 -2410.950000 776.618000 186.569000 | ||
| + | 538.177000 -1556.390000 2774.820000 1342.150000 -4350.580000 -378.349000 1186.870000 -2627.670000 619.576000 60.747200 | ||
| + | 466.937000 -1725.230000 3004.230000 1525.800000 -4514.230000 -370.642000 1165.460000 -2520.760000 654.709000 54.430900 | ||
| + | </pre> | ||
| + | <br> | ||
| + | |||
| + | <div>なお、[[:Media:Input-PCA.zip|入力ファイル]]に対して[[:Media:Mikefile-PCA.zip|こちらのMakefile]]を使って下記のコマンドを入力すれば、ここまでの手順を実施することが出来ます。</div> | ||
| + | <br> | ||
| + | |||
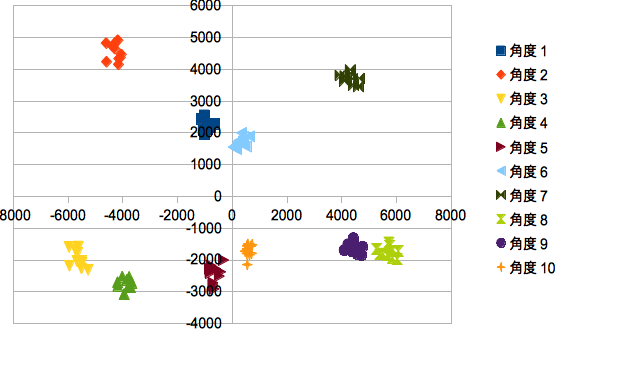
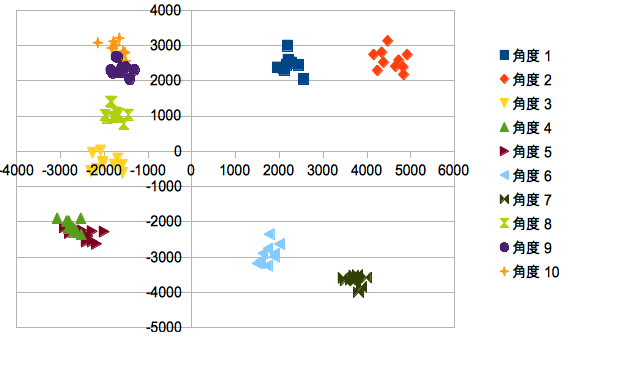
| + | <div>このファイルの10行(角度毎)をひとまとめとして、各列を軸とした散布図を作ってみます。</div> | ||
| + | <table> | ||
| + | <tr> | ||
| + | <td><p align="Center">[[画像:Output-PCA.png]]</p> </td> | ||
| + | </tr> | ||
| + | <tr> | ||
| + | <td><p align="Center">第1主成分(横)と第2主成分(縦)の散布図</p> </td> | ||
| + | </tr> | ||
| + | </table> | ||
| + | <br> | ||
| + | |||
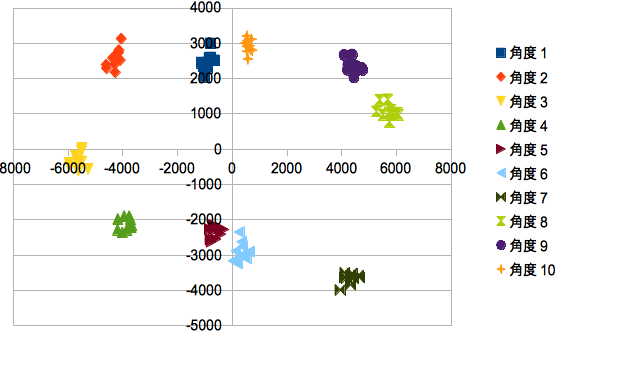
| + | <table> | ||
| + | <tr> | ||
| + | <td><p align="Center">[[画像:Output1-PCA.png]]</p> </td> | ||
| + | </tr> | ||
| + | <tr> | ||
| + | <td><p align="Center">第1主成分(横)と第3主成分(縦)の散布図</p> </td> | ||
| + | </tr> | ||
| + | </table> | ||
| + | <br> | ||
| + | |||
| + | <table> | ||
| + | <tr> | ||
| + | <td><p align="Center">[[画像:Output2-PCA.png]]</p> </td> | ||
| + | </tr> | ||
| + | <tr> | ||
| + | <td><p align="Center">第2主成分(横)と第3主成分(縦)の散布図</p> </td> | ||
| + | </tr> | ||
| + | </table> | ||
| + | <br> | ||
| + | |||
| + | <div>散布図を基に画像を分類します。10通りであれば、ほぼ三次元で分類できていることが分かります。</div> | ||
<br> | <br> | ||
2014年8月4日 (月) 09:30時点における最新版
主成分分析(Principal Component Analysis)とは、多変量を要素としてもつベクトルデータの集合に対して、多変量空間の中で、各ベクトルデータをある軸に投影した場合に最も大きな分散をもつ軸(主軸)を求め、順次、それと直交する(無相関の)軸で、最も大きな分散を持つ軸を求めていく手法である。計算を打ち切った場合に、それ以降の情報は誤差として取り扱われる。
主成分分析の実行例
画像毎の主成分分析
主にmrcImagePCAを使用して、複数画像の分類を行います。
入力ファイルの画像
10通りの回転(縦)画像に10通りのノイズ(横)をそれぞれ掛けています。(計100個)
まず、mrcImagePCAを使用して主軸を求めます。
NO2_ROI_LISTのデータ
Target-1-0-0-0.nroi Target-1-0-0-1.nroi Target-1-0-0-2.nroi Target-1-0-0-3.nroi Target-1-0-0-4.nroi Target-1-0-0-5.nroi Target-1-0-0-6.nroi Target-1-0-0-7.nroi Target-1-0-0-8.nroi Target-1-0-0-9.nroi Target-37-0-0-0.nroi Target-37-0-0-1.nroi -中略- Target-289-0-0-8.nroi Target-289-0-0-9.nroi Target-325-0-0-0.nroi Target-325-0-0-1.nroi Target-325-0-0-2.nroi Target-325-0-0-3.nroi Target-325-0-0-4.nroi Target-325-0-0-5.nroi Target-325-0-0-6.nroi Target-325-0-0-7.nroi Target-325-0-0-8.nroi Target-325-0-0-9.nroi
TEST_PCA_LISTのデータ
Target-1-0-0-0.tpca Target-1-0-0-1.tpca Target-1-0-0-2.tpca Target-1-0-0-3.tpca Target-1-0-0-4.tpca Target-1-0-0-5.tpca Target-1-0-0-6.tpca Target-1-0-0-7.tpca Target-1-0-0-8.tpca Target-1-0-0-9.tpca Target-37-0-0-0.tpca Target-37-0-0-1.tpca -中略- Target-289-0-0-8.tpca Target-289-0-0-9.tpca Target-325-0-0-0.tpca Target-325-0-0-1.tpca Target-325-0-0-2.tpca Target-325-0-0-3.tpca Target-325-0-0-4.tpca Target-325-0-0-5.tpca Target-325-0-0-6.tpca Target-325-0-0-7.tpca Target-325-0-0-8.tpca Target-325-0-0-9.tpca
コマンド
mrcImagePCA -i NO2_ROI_LIST -o TEST_PCA_LIST -NX 39 -NY 39 -numE 20 -O EIGEN_INFO -E eigen -EPS 100;
コマンド実行後に固有値を確認します。
EIGEN_INFOのデータ
0 485 13783745.48 16.25 1 600 6874158.21 24.36 2 997 6040647.42 31.48 3 529 5425460.64 37.88 4 834 4720681.32 43.45 5 879 3932086.98 48.08 6 842 3632776.78 52.37 7 645 3182620.81 56.12 8 566 2449230.98 59.01 9 1116 1328891.76 60.57 10 1031 1287023.24 62.09 11 579 1257054.49 63.57 12 1080 1214056.15 65.01 13 856 1161105.65 66.38 14 934 1144996.99 67.73 -以下略-
固有値(第3列目)が高い順にデータが並んでいます。下図をご覧下さい。今回は第8成分当たりまでの固有値が高くなっています。60%の分散まで説明できることが分かります。
第1 ~ 3主成分にて散布図の様子を見てみます。
mrcImagePCAのオプション-o で指定したファイルには固有値が高い順にそれぞれの画像毎のベクトル成分が格納されています。よって、このデータの上位部分を使って画像がどのグループに属しているかを見ることができます。mrcImageMakeDumpを使うと、mrcImageのデータをASCIIとして取り出すことができます。
-1002.110000 1962.390000 2375.080000 3780.900000 1531.830000 -3511.960000 -524.329000 1190.540000 -1106.170000 337.342000 -1111.780000 2439.510000 2452.540000 3826.020000 1630.650000 -3519.130000 -457.767000 1531.510000 -316.514000 -2399.750000 -844.584000 2207.500000 2577.200000 3895.480000 1722.810000 -3401.740000 -573.914000 961.414000 -1120.780000 75.002400 -897.296000 2107.620000 2308.710000 3974.960000 1590.460000 -3559.020000 -836.757000 1690.460000 -332.499000 46.332400 -639.501000 2286.200000 2513.990000 3868.320000 1741.350000 -3316.310000 -553.213000 1443.870000 -1044.260000 560.677000 -1015.980000 2549.020000 2049.920000 3854.560000 1503.460000 -3118.820000 -919.956000 1212.420000 -792.175000 1047.500000 -892.673000 2168.280000 2455.920000 3951.430000 1400.510000 -3498.790000 -528.413000 1509.180000 -1141.580000 10.826800 -799.775000 2190.870000 2994.040000 3730.140000 1208.160000 -3002.190000 -538.733000 800.946000 -1115.250000 380.240000 -1061.460000 2100.710000 2348.670000 3881.800000 1573.210000 -3440.970000 -606.476000 1363.520000 -649.180000 422.532000 -782.003000 2198.650000 2594.880000 3976.130000 1891.720000 -3371.260000 -531.849000 1410.830000 -957.755000 148.813000 -4295.390000 4650.010000 2406.060000 -2699.870000 1602.340000 2108.780000 1198.180000 -963.790000 565.743000 256.211000 -4371.810000 4724.700000 2581.440000 -2274.290000 1625.690000 1392.540000 1677.500000 -492.734000 770.713000 -2612.010000 -中略- 533.205000 -1655.000000 3206.460000 1451.350000 -4268.840000 -120.817000 900.958000 -2478.230000 428.414000 361.083000 667.314000 -1569.670000 2828.330000 1229.300000 -4102.610000 -108.603000 1067.760000 -2409.760000 875.312000 -147.388000 703.368000 -1789.180000 3114.700000 1694.560000 -4408.100000 -286.116000 1112.690000 -2717.040000 595.316000 -136.777000 546.967000 -2147.200000 3076.260000 1691.570000 -4386.750000 -567.557000 963.625000 -2624.400000 913.221000 -49.355200 567.210000 -1505.020000 2555.640000 1290.990000 -4242.580000 -407.482000 1022.360000 -2779.230000 636.427000 308.664000 727.232000 -1522.510000 2804.310000 1861.250000 -4377.870000 -163.006000 1417.020000 -2410.950000 776.618000 186.569000 538.177000 -1556.390000 2774.820000 1342.150000 -4350.580000 -378.349000 1186.870000 -2627.670000 619.576000 60.747200 466.937000 -1725.230000 3004.230000 1525.800000 -4514.230000 -370.642000 1165.460000 -2520.760000 654.709000 54.430900
なお、入力ファイルに対してこちらのMakefileを使って下記のコマンドを入力すれば、ここまでの手順を実施することが出来ます。
このファイルの10行(角度毎)をひとまとめとして、各列を軸とした散布図を作ってみます。
第1主成分(横)と第2主成分(縦)の散布図 |
第1主成分(横)と第3主成分(縦)の散布図 |
第2主成分(横)と第3主成分(縦)の散布図 |
散布図を基に画像を分類します。10通りであれば、ほぼ三次元で分類できていることが分かります。