Principal Component Analysis
From EosPedia
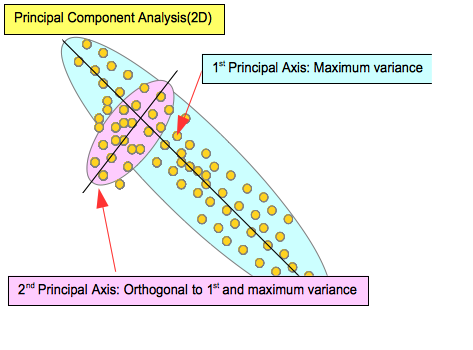
Principal Component Analysis is the method that calculates from vector data set which has elements of Multivariate to the axis (principal axis) which has maximum variance when each vector data is projected into that axis on Multivariate Space, and calculates the axis sequentially that is orthogonal(no correlation) to it and has largest variance.
Execution example of PCA
PCA of each image
Classify multiple images by using mrcImagePCA mainly.
Input file's image
rotate the image at 10 pattern (vertical), and add noise at 10 pattern (Horizontal). (Sum 100)
First, calculates principal axis by using mrcImagePCA.
NO2_ROI_LIST's data
Target-1-0-0-0.nroi Target-1-0-0-1.nroi Target-1-0-0-2.nroi Target-1-0-0-3.nroi Target-1-0-0-4.nroi Target-1-0-0-5.nroi Target-1-0-0-6.nroi Target-1-0-0-7.nroi Target-1-0-0-8.nroi Target-1-0-0-9.nroi Target-37-0-0-0.nroi Target-37-0-0-1.nroi ... Target-289-0-0-8.nroi Target-289-0-0-9.nroi Target-325-0-0-0.nroi Target-325-0-0-1.nroi Target-325-0-0-2.nroi Target-325-0-0-3.nroi Target-325-0-0-4.nroi Target-325-0-0-5.nroi Target-325-0-0-6.nroi Target-325-0-0-7.nroi Target-325-0-0-8.nroi Target-325-0-0-9.nroi
TEST_PCA_LIST's data
Target-1-0-0-0.tpca Target-1-0-0-1.tpca Target-1-0-0-2.tpca Target-1-0-0-3.tpca Target-1-0-0-4.tpca Target-1-0-0-5.tpca Target-1-0-0-6.tpca Target-1-0-0-7.tpca Target-1-0-0-8.tpca Target-1-0-0-9.tpca Target-37-0-0-0.tpca Target-37-0-0-1.tpca ... Target-289-0-0-8.tpca Target-289-0-0-9.tpca Target-325-0-0-0.tpca Target-325-0-0-1.tpca Target-325-0-0-2.tpca Target-325-0-0-3.tpca Target-325-0-0-4.tpca Target-325-0-0-5.tpca Target-325-0-0-6.tpca Target-325-0-0-7.tpca Target-325-0-0-8.tpca Target-325-0-0-9.tpca
Command
mrcImagePCA -i NO2_ROI_LIST -o TEST_PCA_LIST -NX 39 -NY 39 -numE 20 -O EIGEN_INFO -E eigen -EPS 100;
Check the eigenvalues after command run.
EIGEN_INFO's data
0 485 13783745.48 16.25 1 600 6874158.21 24.36 2 997 6040647.42 31.48 3 529 5425460.64 37.88 4 834 4720681.32 43.45 5 879 3932086.98 48.08 6 842 3632776.78 52.37 7 645 3182620.81 56.12 8 566 2449230.98 59.01 9 1116 1328891.76 60.57 10 1031 1287023.24 62.09 11 579 1257054.49 63.57 12 1080 1214056.15 65.01 13 856 1161105.65 66.38 14 934 1144996.99 67.73 ...
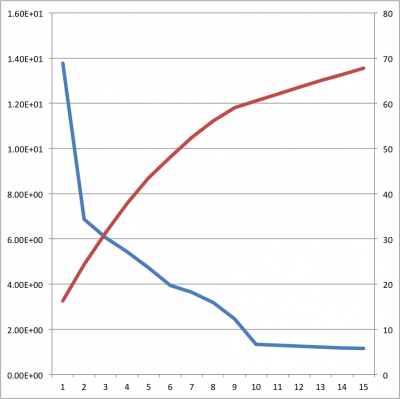
Data are arranged in the order of height of the eigenvalues (3rd columns). See the figure below. In this case, Eigenvalues of up to the 8th component is higher than others. You can see that it can be explained up to 60% dispersion.
Look about the scatter plot at 1st ~ 3rd component.
The file specified at mrcImagePCA's option -o is stored the vector elements of each image in the order of height of the eigenvalues. Thus, by using upper level of this data, you can see which group the image is belong. In addition, by using mrcImageMakeDump, mrcImage's data can be output as ASCII.
-1002.110000 1962.390000 2375.080000 3780.900000 1531.830000 -3511.960000 -524.329000 1190.540000 -1106.170000 337.342000 -1111.780000 2439.510000 2452.540000 3826.020000 1630.650000 -3519.130000 -457.767000 1531.510000 -316.514000 -2399.750000 -844.584000 2207.500000 2577.200000 3895.480000 1722.810000 -3401.740000 -573.914000 961.414000 -1120.780000 75.002400 -897.296000 2107.620000 2308.710000 3974.960000 1590.460000 -3559.020000 -836.757000 1690.460000 -332.499000 46.332400 -639.501000 2286.200000 2513.990000 3868.320000 1741.350000 -3316.310000 -553.213000 1443.870000 -1044.260000 560.677000 -1015.980000 2549.020000 2049.920000 3854.560000 1503.460000 -3118.820000 -919.956000 1212.420000 -792.175000 1047.500000 -892.673000 2168.280000 2455.920000 3951.430000 1400.510000 -3498.790000 -528.413000 1509.180000 -1141.580000 10.826800 -799.775000 2190.870000 2994.040000 3730.140000 1208.160000 -3002.190000 -538.733000 800.946000 -1115.250000 380.240000 -1061.460000 2100.710000 2348.670000 3881.800000 1573.210000 -3440.970000 -606.476000 1363.520000 -649.180000 422.532000 -782.003000 2198.650000 2594.880000 3976.130000 1891.720000 -3371.260000 -531.849000 1410.830000 -957.755000 148.813000 -4295.390000 4650.010000 2406.060000 -2699.870000 1602.340000 2108.780000 1198.180000 -963.790000 565.743000 256.211000 -4371.810000 4724.700000 2581.440000 -2274.290000 1625.690000 1392.540000 1677.500000 -492.734000 770.713000 -2612.010000 ... 533.205000 -1655.000000 3206.460000 1451.350000 -4268.840000 -120.817000 900.958000 -2478.230000 428.414000 361.083000 667.314000 -1569.670000 2828.330000 1229.300000 -4102.610000 -108.603000 1067.760000 -2409.760000 875.312000 -147.388000 703.368000 -1789.180000 3114.700000 1694.560000 -4408.100000 -286.116000 1112.690000 -2717.040000 595.316000 -136.777000 546.967000 -2147.200000 3076.260000 1691.570000 -4386.750000 -567.557000 963.625000 -2624.400000 913.221000 -49.355200 567.210000 -1505.020000 2555.640000 1290.990000 -4242.580000 -407.482000 1022.360000 -2779.230000 636.427000 308.664000 727.232000 -1522.510000 2804.310000 1861.250000 -4377.870000 -163.006000 1417.020000 -2410.950000 776.618000 186.569000 538.177000 -1556.390000 2774.820000 1342.150000 -4350.580000 -378.349000 1186.870000 -2627.670000 619.576000 60.747200 466.937000 -1725.230000 3004.230000 1525.800000 -4514.230000 -370.642000 1165.460000 -2520.760000 654.709000 54.430900
Incidentally, by using Input fileに対してThis Makefile and running at the following commands, you can execute the method of up to here.
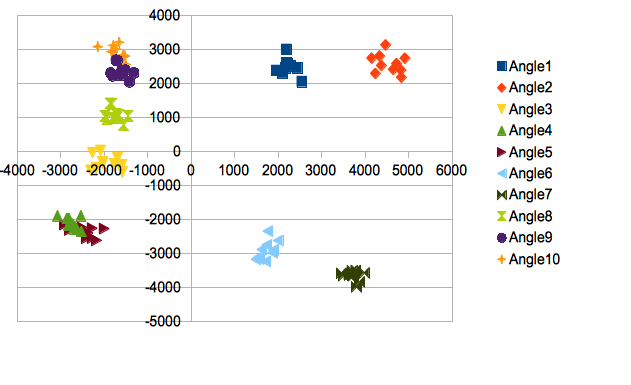
Collect 10 rows of this file as 1 angle's data, and display the scatter plot whose axis is as each column.
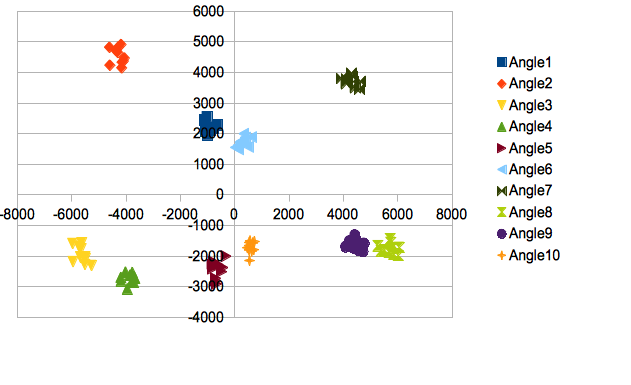
the scatter plot by 1st(Vertical) and 2nd(Horizontal) |
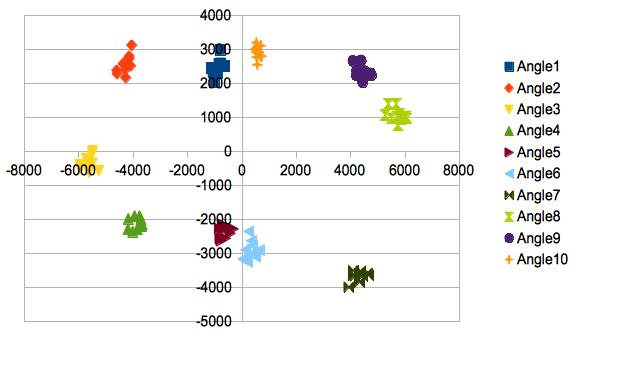
the scatter plot by 1st(Vertical) and 3rd(Horizontal) |
the scatter plot by 2nd(Vertical) and 3rd(Horizontal) |
Classify the images based on the scatter plot. If its pattern is above 10, it means that on 3D they can be almost classified.