pdb2mrc2d

pdb2mrc2dはPDBファイルをmrcImageファイルに変換するEosのコマンド。

オプション一覧

メインオプション

オプション	必須項目/選択項目	説明	デフォルト
-i	必須	入力ファイル設定: PDB	NULL
-o	選択	出力ファイル設定: mrcImage(2D)	NULL
-O	選択	出力ファイル設定: mrcImage(3D)	NULL
-d	必須	1ピクセルの幅を指定	5.0 5.0
-s	選択	画像の位置を指定	0.0 0.0
-n	必須	画像のサイズを指定	0 0
-Rot	選択	回転（ｘ軸、ｙ軸のみ）	1 1
-S	選択	Z軸→X軸→Y軸の順で回転	0.0 0.0 0.0
-startEA	選択	オイラー角を設定	YOYS 0.0 0.0 0.0
-EAMode	選択	RotationModeを指定	YOYS
-EARot1	選択	主となる回転	5.0 0.0 180.0
-EARot2	選択	-EARot1とは別の回転	5.0 0.0 180.0
-w	選択	重みを設定	1.0
-sig	選択	原子の半径を指定: w* exp (- x^2 / (2*sig^2) )	0.0: 0の場合は、点として取り扱う
-m	選択	モード設定	0
-h	選択	ヘルプを表示

モードの詳細

モード	説明
0	メルカトール図法・等角
1	モルワイデ図法・等角
2	メルカトール図法・等積
3	モルワイデ図法・等積

※オプション-Sと-startEAの両方が宣言されていた場合、-Sを実行した後に-startEAが実行される
※軸を中心にもってきたい場合は、pdbInfoで軸を調べ、pdbMoveで軸の＋とーを逆にして実行する

RotModeの設定の詳細

一桁目：	どの軸から回転を始めるか設定
二桁目：	回転軸の順番を設定１
	O…Z→Y→Xの順に回転軸を変更する E…Z→X→Yの順に回転軸を変更する
三桁目：	回転軸の順番の設定２
	Y…順番を維持する N…順番を逆順にする
四桁目：	回転方法を設定
	Y…物体そのものをまわす D…座標を移動させる

実行例

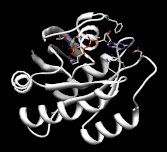
入力ファイルの画像

pdbInfoでみた入力ファイルの詳細

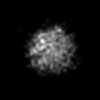
出力ファイルの画像

オプションを使用し、画像に物体が写るよう調整する
今回の入力ファイルでは下記のようにオプションを設定すると、物体がほぼ中心に写る

-d	0.8 0.8
-s	-40 -40
-n	100 100

出力ファイル→2D

出力ファイル→3D

このオプションを使用した場合、二つの画像に相違点はない

オプション　-Rot

-Rot 6 6に設定

出力ファイル→2D

出力ファイル→3D（2Dの結果を繋ぎ、3Dで出力している）

ｘｙ平面の図	ｙｚ平面の図

オプション　-S

-Rot 6 6、-S 30 30 30に設定

出力ファイル→2D

オプション　-startEA

-Rot 6 6、-startEA XOYS 30 30 30に設定

出力ファイル→2D

オプション　-EAMode

-Rot 6 6、-EAMode XOYSに設定

出力ファイル→2D

-Rot 6 6、-EAMode YOYSに設定

出力ファイル→2D

オプション　-EARot1,-EARot2

-EARot1 10 20 70,-EARot2 20 50 100に設定

出力ファイル→2D

オプション　-sig

-sig 1に設定、出力ファイルは-oとする

オプション　-w

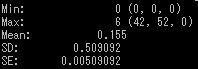
-wを指定しなかった場合の画像データ

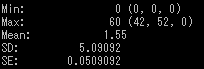
-w 10を指定した場合の画像データ

オプション　-m

m=0で実行
m=1で実行
	ファイル:m1-pdb2mrc2d.png
m=2で実行
	ファイル:m2-pdb2mrc2d.png
m=3で実行
	ファイル:m3-pdb2mrc2d.png

今回の画像では変化がわかりづらいが、画像データの詳細を見ると、変化があることが分かる