「電子線トモグラフィー」の版間の差分

2014年7月14日 (月) 01:14時点における版

電子線トモグラフィーとは、電子顕微鏡を用いた３次元再構成法の一つで、同一視野を様々な方向からの投影された電子顕微鏡像をコンピュータの中で三次元像に再構成し、コンピュータを使って断層像（トモグラム）を作成する手法です。

　下記にその手順を順に述べていきます。

1 連続傾斜像の撮影
2 画像の補正
3 ラフ・アラインメント
- 3.1 前処理(窓関数)
- 3.2 位置合わせ
  - 3.2.1 mrcImageCorrelationを使用した場合
    - 3.2.1.1 実行例1
4 ファイン・アラインメント
- 4.1 実行例1
- 4.2 実行例2(繰り返し)
5 ３次元再構成
- 5.1 mrc2Dto3Dで実行
- 5.2 ラドン変換を使った３次元再構成で実行
  - 5.2.1 実行例1
  - 5.2.2 実行例2
6 電子線トモグラフィー画像のもつ問題点
- 6.1 ミッシングエリア
- 6.2 画像の位置、フォーカスの問題
  - 6.2.1 平行移動の補正
  - 6.2.2 軸の決定
7 トモグラフに使われる画像処理
- 7.1 平滑化
  - 7.1.1 実行例1
- 7.2 セグメンテーション
  - 7.2.1 ３次元画像の切り出し
    - 7.2.1.1 実行例1
  - 7.2.2 ２次元画像の切り出し
    - 7.2.2.1 実行例1
    - 7.2.2.2 実行例2(2軸投影)
8 トモグラム画像の解釈
- 8.1 サブトモグラムの平均化
  - 8.1.1 実行例1
  - 8.1.2 実行例2

連続傾斜像の撮影

　この手法で撮影すると試料を特定の軸に対して一定間隔で傾斜した画像になります。また、傾斜角度が大きくなるにつれて視野は広くなるので、映っている物体は傾斜軸の中心に集まってきます。

１軸傾斜

２軸傾斜の画像を得るときはときは試料を90°回転させて、1軸傾斜と同様の方法で撮影します。

２軸傾斜(試料を90°回転してから傾斜を行う)

画像の補正

　傾斜画像では、視野全体がアンダーフォーカスとなるように、通常の電子顕微鏡撮影よりも大きなデフォカース値をとる場合が多いです。その場合、LaB6などの電子銃では第一トーンリングより外側の情報がほとんど無いために、CTF補正等は必要ありませんが、電界放出銃を利用した場合には、場合によっては間違った情報を与える場合があるので注意が必要です。

ラフ・アラインメント

　傾斜画像の中心付近の画像の相関から、それぞれの傾斜画像の大まかな位置を合わせます。

入力ファイル(Y軸周りに±60°の範囲で2°刻みで回転)

10°刻みで表示

前処理(窓関数)

　窓関数を掛けて画像端のノイズを除去します。

今回は横80%、縦90%の窓関数を掛けます。

コマンド(1枚目の場合): mrcImageWindowing -i Set1000.roi -o Set1000.mask -W 0.2 0.2 0.1 0.1

こちらのMakefileを使用すると全てのroiファイルについて処理を行います。

設定内容

# For Windowing
WIN_X=0.2
WIN_X_MAX=0.2
WIN_Y=0.1
WIN_Y_MAX=0.1
WIN_MODE=18

コマンド

make Windowing

出力ファイル

10°刻みで表示

位置合わせ

　傾斜角度に応じて対象が平行移動しているので、位置を合わせます。このとき傾斜による影響を受けにくくするために隣同士の角度で位置合わせを行います。

例. 2°刻みで撮影した画像の場合
　2°画像の位置を0°画像の位置に合わせる
　4°画像の位置を位置補正後の2°画像の位置に合わせる
　6°画像の位置を位置補正後の4°画像の位置に合わせる
　.
　.

　(+が終わったら-についても同様に位置を合わせる)

mrcImageCorrelationを使用した場合

　こちらのMakefileを使用して位置合わせを実行します。Makefileを使用せずにコマンドを逐次入力しても位置合わせは可能ですが、mrc2Dto3D用の入力ファイルリストを作成する必要があります。

実行例1

入力ファイル

10°刻みで表示

コマンド

make CorFit1

出力ファイル

10°刻みで表示

ファイン・アラインメント

　傾斜画像の軸の位置、角度を出来る限り一致させます。

実行例1

　軸の傾きはmrcImageTiltAxisSearchで算出することができます。

入力ファイル(傾斜軸を10°傾けた１軸傾斜のデータ)

10°刻みで表示

使用Makefileの設定

# RotMode
ROTMODE=ZOYS
# Rot1
ROT1MIN=10
ROT1MAX=10
ROT1D=10
# Rot2
ROT2MIN=-60
ROT2MAX=60
ROT2D=2
# Rot3
ROT3MIN=0
ROT3MAX=0
ROT3D=30
### For mrcImageMove
SHIFT2MAX=10
SHIFT3MAX=0
### For mrcImageTiltAxisSearch
TILTMIN=0
TILTMAX=20
TILTD=2

コマンド

make TiltFit

出力した軸の傾き(.tiltinfoファイルに格納される)

9.895

３次元再構成したときの違い

補正前

補正後

xy平面	yz平面	zx平面

実行例2(繰り返し)

出力された軸の傾きを中心として、繰り返しmrcImageTiltAxisSearchを使用します。

入力ファイル(傾斜軸を1°傾けた１軸傾斜のデータ)

10°刻みで表示

使用Makefileの設定

# For mrcImageTiltAxisSearch
IN_TILT_EXT=roi
# RotMode
ROTMODE=ZOYR
# Rot1
ROT1MIN=10
ROT1MAX=10
ROT1D=10
# Rot2
ROT2MIN=-60
ROT2MAX=60
ROT2D=10
# Rot3
ROT3MIN=0
ROT3MAX=0
ROT3D=10
### For mrcImageTiltAxisSearch
TILTMIN=-10
TILTMAX=10
TILTN=10
TILTITER=100
TILTSCALE=5

コマンド

make TiltFit

軸の傾きの遷移

0.084
0.161
0.230
0.294
0.345

-中略-

0.701
0.700
0.685
0.706
0.701

傾斜軸の傾きが1付近に近づきます。

３次元再構成

　２次元画像のセットから３次元画像を再構成します。

元の3Dデータの画像

xy平面

yz平面

zx平面

最小

最大
平均値
標準偏差

標準誤差

0 (0, 0, 0)

4 (31, 26, 26)
0.0116844
0.147033

0.000287174

mrc2Dto3Dで実行

実行例1

　連続傾斜像の撮影で軸にズレがない場合は角度刻みをそのまま入力ファイルリストに設定します。

入力ファイル

10°刻みで表示

コマンド: mrc2Dto3D -i Input.3dlst -o Input.3d -m 1

こちらのMakefileを使用すれば、以下のコマンドでも実行できます。

設定内容

# For Reconstruction
IN_3D_EXT=fit
# RotMode
ROTMODE=YOYS
# Rot1
ROT1MIN=-60
ROT1MAX=60
ROT1D=2
# Rot2
ROT2MIN=0
ROT2MAX=0
# Rot3
ROT3MIN=0
ROT3MAX=0

コマンド

make 3DList
make Input.3d

出力ファイル

xy平面

yz平面

zx平面

最小

最大
平均値
標準偏差

標準誤差

-0.00437076 (39, 34, 36)

0.00799233 (37, 34, 36)
3.45089e-06
0.000342836

6.69601e-07

実行例2(２軸傾斜)

２軸で傾斜した画像にて３次元再構成を行います。

入力ファイル(X, Y軸周りに±60°の範囲でそれぞれ10°刻みで傾斜)

1行目がX軸傾斜、２行目がY軸傾斜

こちらのMakefileを使って３次元再構成を行います。

コマンド

make all

出力ファイル

xy平面

yz平面

zx平面

最小

最大
平均値
標準偏差

標準誤差

-8.93723 (34, 27, 31)

22.0455 (39, 38, 29)
0.0250646
1.38992

0.00271469

実行例3(Double)

mrc2Dto3Dのオプション -Doubleを使用して３次元再構成を行います。

変更箇所

.roilst.mrc3d:
#	mrc2Dto3D -I $*.roilst -o $*.mrc3d -single 0 -InterpolationMode 2 -m 1 
	mrc2Dto3D -I $*.roilst -o $*.mrc3d -Double -InterpolationMode 2 -m 1

出力ファイル

xy平面

yz平面

zx平面

最小

最大
平均値
標準偏差

標準誤差

-9952.6 (39, 24, 0)

7537.08 (39, 34, 33)
88.9869
684.828

1.33755

ラドン変換を使った３次元再構成で実行

　mrc2Dto3Dを使用するほかにラドン変換から３次元像を作る方法があります。ラドン変換は以下の流れで行います。

位置合わせ済みの2Dリスト
↓mrcImageSinogramCreate
シノグラムリスト
↓mrcRadon2Dto3D
3Dラドンファイル
↓mrcImageInverseRadonTransform

3Dファイル(完了)

実行例1

こちらのMakefileを使い、上記の.roilstファイルについて実行します。

コマンド

make Radon3D

出力ファイル

xy平面	yz平面	zx平面

最小

最大
平均値
標準偏差

標準誤差

1.98221e+06 (63, 3, 33)

1.17729e+07 (35, 32, 32)
3.56296e+06
1.53682e+06

3001.61

実行例2

　逆ラドン変換のオプションを変更したこちらのMakefileを使って実行します。

変更内容

### RadonTransform
RBP_MODE=4
RBP_OPTION=-Rmin 0.05 -Rmax 0.1

.3dradon.3d:
	mrcImageInverseRadonTransform -i $*.3dradon -o $*.3d -bpm $(RBP_MODE) $(RBP_OPTION);

コマンド

make Radon3D

出力ファイル

xy平面	yz平面	zx平面

最小

最大
平均値
標準偏差

標準誤差

-48.3524 (31, 0, 31)

110.505 (34, 19, 37)
0.923644
12.4855

0.0243857

電子線トモグラフィー画像のもつ問題点

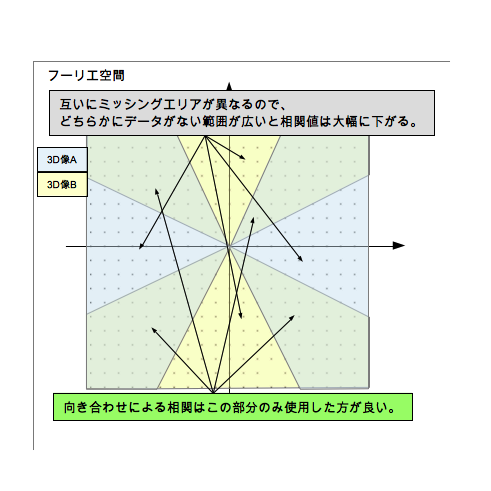
ミッシングエリア

　全方位からの投影像を得られないために、ミッシングエリア(１軸の場合はウェッジ、２軸の場合はピラミッド)とよばれる情報がない領域があります。そのため、方向依存でのボケを生じます。

元の３次元像

xy平面

yz平面

zx平面

最小

最大
平均値
標準偏差

標準誤差

0 (0, 0, 0)

2 (29, 29, 14)
0.108302
0.364429

0.000711774

使用MakeFileの変更箇所

# Initial Reference Model 
INITIAL=Input-ellipsoidal

# For mrcImageCorrelation
IN_CORR_EXT=roi
IN_CORR_LIST=ROIs

### For mrcImageMove
SHIFT2MAX=0
SHIFT3MAX=0

コマンド

make TestData
make CorFit1
make CorFit2
make 3D

１軸回転で投影して３次元再構成した場合(Y軸: -60° ~ 60°: 10°刻み)

変更箇所

# Rot2
ROT2MIN=-60
ROT2MAX=60
ROT2D=10
# Rot3
ROT3MIN=0
ROT3MAX=0
ROT3D=10

xy平面

yz平面

zx平面

最小

最大
平均値
標準偏差

標準誤差

-0.00196191 (61, 38, 32)

0.00269849 (24, 21, 37)
3.54393e-05
0.000409595

7.99991e-07

２軸回転で投影して３次元再構成した場合(X, Y軸: 各-60° ~ 60°: 10°刻み)

変更箇所

# Rot2
ROT2MIN=-60
ROT2MAX=60
ROT2D=10
# Rot3
ROT3MIN=-60
ROT3MAX=60
ROT3D=10

xy平面

yz平面

zx平面

最小

最大
平均値
標準偏差

標準誤差

-0.00143731 (50, 32, 45)

0.00230465 (53, 31, 37)
4.22143e-05
0.000363364

7.09696e-07

画像の位置、フォーカスの問題

　試料を傾けながら撮影するため回転軸からの距離に応じてレンズとの距離が変化していきます。これによって生じる問題をいかに補正するかも一つのポイントとなります。

平行移動の補正

　回転する角度が大きくなるほど、視野が広くなるため試料は回転軸の方へ近づいていきます。

軸の決定

　撮影した画像は必ずしも設定した軸を中心に回転しているとは限りません。これは電子顕微鏡自体の性能や試料の設置方法などによって多少のズレが生じてしまうからです。

トモグラフに使われる画像処理

　再構成した３次元画像の解析を行う前処理として以下のような処理を施します。

平滑化

　再構成した３次元像のノイズを除去するため平滑化を行います。

実行例1

入力ファイル

xy平面

yz平面

zx平面

最小

最大
平均値
標準偏差

標準誤差

-0.00268221 (76, 92, 66)

0.00642324 (89, 42, 71)
2.0386e-06
0.000254286

1.63933e-07

コマンド: mrcImageSmoothing -i Input-Tomogram3D.mrc -o Input-TomogramSmth.mrc -m 1

出力ファイル

xy平面

yz平面

zx平面

最小

最大
平均値
標準偏差

標準誤差

-0.00136636 (75, 42, 133)

0.00292404 (94, 65, 68)
-9.48921e-07
0.00013513

8.71152e-08

セグメンテーション

　２次元画像や３次元画像を必要な部分ごとに切り出します。

３次元画像の切り出し

　再構成された３次元画像から粒子と考えられる部分などを切り出します。切り出したデータは３次元画像の解析や平均化するときに使用することができます。

実行例1

切り出したい部分の座標、幅が分かっている場合はmrcImageCenterGetを使います。

入力ファイル

xy平面

yz平面

zx平面

最小

最大
平均値
標準偏差

標準誤差

-0.00136636 (75, 42, 133)

0.00292404 (94, 65, 68)
-9.48921e-07
0.00013513

8.71152e-08

コマンド: mrcImageCenterGet -i Input-TomogramSmth.mrc -o Input-TomogramSub.mrc -Cx 67 -Cy 67 -Cz 67 -Nx 27 -Ny 27 -Nz 27

出力ファイル

xy平面

yz平面

zx平面

最小

最大
平均値
標準偏差

標準誤差

-0.0012017 (5, 9, 13)

0.00263957 (13, 6, 15)
2.22923e-05
0.000388094

2.76625e-06

２次元画像の切り出し

　視野全体ではなく、一部だけ再構成するために傾斜画像から部分的に２次元画像を切り出す場合もあります。視野全体の再構成よりもコストが削減されるので、部分的なデータだけあれば十分な場合はこの手法を用います。試料を傾けながら撮影しているので、画像から切り出す位置や角度を画像によって変える必要があります。

実行例1

入力ファイルの画像(一部)(y軸回転: -60° ~ 60°: 2°刻み)

-60°(p1_001.mrc)

0°(p1_031.mrc)

60°(p1_061.mrc)

こちらのMakefileを使用します。

コマンド

make all

コマンドを入力後にDisplay2(2Dビューワー)が開きますので、切り出したい部分(複数可)を選択しInformationファイル(.roiinfo)を作成します。


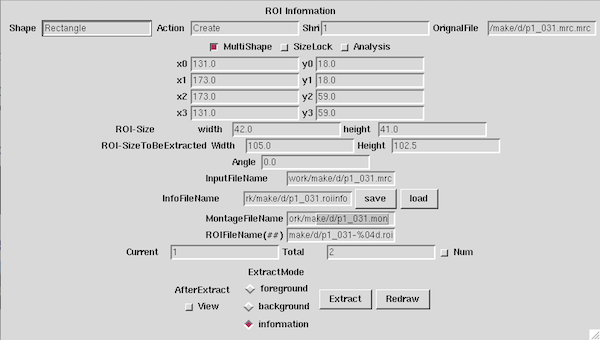
切り出し部分決めてEdit->OKで決定します。	複数切り出したいときはROI->MultiROIを選択します。

今回はInformationだけ作成すれば、切り出しは自動で行われます。

ROI InformationウィンドウにてInfoFileName右側のsaveボタンを押すとファイルが作成されます。

(またはExtractModeをInformationにしてExtractボタンを押します。)

今回出力したInformationファイル

p1_031-0000.roi	Rect	20	30	60	30	60	70	20	70
p1_031-0001.roi	Rect	15	75	55	75	55	115	15	115
p1_031-0002.roi	Rect	25	110	65	110	65	150	25	150
p1_031-0003.roi	Rect	45	0	85	0	85	40	45	40
p1_031-0004.roi	Rect	60	50	100	50	100	90	60	90
p1_031-0005.roi	Rect	55	80	95	80	95	120	55	120
p1_031-0006.roi	Rect	55	120	95	120	95	160	55	160
p1_031-0007.roi	Rect	85	15	125	15	125	55	85	55
p1_031-0008.roi	Rect	85	51	125	51	125	91	85	91
p1_031-0009.roi	Rect	85	91	125	91	125	131	85	131
p1_031-0010.roi	Rect	93	130	133	130	133	170	93	170
p1_031-0011.roi	Rect	115	25	155	25	155	65	115	65
p1_031-0012.roi	Rect	120	60	160	60	160	100	120	100
p1_031-0013.roi	Rect	123	100	163	100	163	140	123	140
p1_031-0014.roi	Rect	115	140	155	140	155	180	115	180
p1_031-0015.roi	Rect	152	152	192	152	192	192	152	192

1枚の画像についてDisplay2からInformationファイル(.roiinfo)を作成すると、残りの画像については傾きから切り出す範囲を計算し、自動で切り出しが行われます。

自動で切り出された画像(縦: 選択範囲毎, 横: ファイル(角度)毎)


-60°	0°	60°

切り出し処理を終えた後はそれぞれの画像に対して３次元再構成が行われます。

再構成されたそれぞれの３次元画像

xy平面
yz平面
zx平面

実行例2(2軸投影)

　２軸で投影した画像から切り出し及び再構成を行ってみます。

入力ファイルの画像(一部)(x軸, y軸回転: -60° ~ 60°: 10°刻み)

x軸回転	-60°	0°	60°
y軸回転	-60°	0°	60°

こちらのMakefileを使用します。

コマンド

make all

今回はこの領域でROIファイルの切り出しを行います。

今回出力したInformationファイル

DataA_006-0000.roi Rect        0.722314      137.147614       33.000000      106.000000       49.053597      122.636041       16.775911      153.783654
DataA_006-0001.roi Rect       15.000000       79.000000       42.000000       79.000000       42.000000      107.000000       15.000000      107.000000
DataA_006-0002.roi Rect       13.000000       39.000000       58.000000       39.000000       58.000000       64.000000       13.000000       64.000000
DataA_006-0003.roi Rect       41.000000      129.000000       84.000000      129.000000       84.000000      154.000000       41.000000      154.000000
DataA_006-0004.roi Rect       51.000000       85.000000       82.000000       85.000000       82.000000      119.000000       51.000000      119.000000
DataA_006-0005.roi Rect       47.269722       69.494676       78.455043       40.316766       95.000000       58.000000       63.814679       87.177909
DataA_006-0006.roi Rect       66.000000        4.000000       92.000000        4.000000       92.000000       44.000000       66.000000       44.000000
DataA_006-0007.roi Rect       77.597890      150.922358       95.484138      132.052220      120.886248      156.129861      103.000000      175.000000
DataA_006-0008.roi Rect       93.000000       92.000000      115.000000       92.000000      115.000000      132.000000       93.000000      132.000000
DataA_006-0009.roi Rect      100.000000       51.000000      121.000000       51.000000      121.000000       93.000000      100.000000       93.000000
DataA_006-0010.roi Rect       98.589377       19.087800      119.760822       10.100593      135.000000       46.000000      113.828555       54.987208
DataA_006-0011.roi Rect      122.000000      141.000000      146.000000      141.000000      146.000000      184.000000      122.000000      184.000000
DataA_006-0012.roi Rect      136.883039       95.213292      160.000000      104.000000      144.116961      145.786708      121.000000      137.000000
DataA_006-0013.roi Rect      127.000000       73.000000      146.061183       60.635990      169.000000       96.000000      149.938817      108.364010
DataA_006-0014.roi Rect      140.000000       22.000000      177.361289       43.286947      166.470292       62.402025      129.109004       41.115078
DataA_006-0015.roi Rect      163.000000      152.000000      183.000000      152.000000      183.000000      190.000000      163.000000      190.000000

自動で切り出された画像(縦: 選択範囲毎, 横: ファイル(角度)毎)

DataA(x軸回転)

DataB(y軸回転)

切り出しサイズがバラバラで分かりにくくなっていますが、いずれの傾斜軸でもROIファイルが自動で切り出されています。

再構成されたそれぞれの３次元画像

xy平面
yz平面
zx平面

トモグラム画像の解釈

　また、多様な構造を含むため、３次元画像から興味あるセグメントを切り出すなどの作業が必要です。そのための支援ソフトウェアが必要です。

サブトモグラムの平均化

　セグメンテーションによって分割された３次元データ同士が別方向を向いている同じ粒子であるとき、それを平均化することでミッシングエリアを補間し、より精密な３次元像にすることができます。

分割したデータ1

分割したデータ2(90°向きが違う)

平均したデータ


xy平面	yz平面	zx平面

実行例1

入力ファイル

xy平面
yz平面
zx平面

３次元像を平均化する前にmrcImageAutoRotationCorrelation3Dを使って、向きを合わせます。

参照ファイル(入力ファイルの真ん中のデータを使用)

xy平面

yz平面

zx平面

最小

最大
平均値
標準偏差

標準誤差

-0.0012017 (5, 9, 13)

0.00263957 (13, 6, 15)
2.22923e-05
0.000388094

2.76625e-06

コマンド: mrcImageAutoRotationCorrelation3D -i c1-1.mrc -r c2-2.mrc -fit f1-1.mrc -EA YOYS -Rot1 0 0 30 -Rot2 0 330 30 -Rot3 0 330 30 -Xrange 0 0 -Yrange 0 0 -Zrange 0 0

補正後のデータ(-fitの出力ファイル)

xy平面
yz平面
zx平面

補正ファイルに対し、mrcImageAverageにて平均化を行います。

出力ファイル

xy平面

yz平面

zx平面

最小

最大
平均値
標準偏差

標準誤差

-0.000536652 (6, 13, 12)

0.00177258 (13, 17, 13)
3.22171e-05
0.000228739

1.6304e-06

平均化することにより３次元像の質(特にyz平面)が良くなりました。

実行例2

入力ファイル

xy平面
yz平面
zx平面

参照ファイル(入力ファイルの先頭のデータを使用)

xy平面

yz平面

zx平面

最小

最大
平均値
標準偏差

標準誤差

-5.47817 (34, 19, 20)

16.0715 (31, 22, 19)
0.142234
1.22547

0.0048441

同様にまず向きを合わせます。

コマンド: mrcImageAutoRotationCorrelation3D -i p1-0001.mrc3d -r Target.mrc3dref -fit p1-0001.3dfit -EA XEYR -Rot1 0 355 5 -Rot2 0 355 5 -Rot3 0 0 30 -M 18

補正後のデータ(-fitの出力ファイル)

xy平面
yz平面
zx平面

参照ファイルに向きを合っているものと合っていないものがあります。
これはそれぞれのサブトモグラムの３次元像にてミッシングエリアが異なるので、どちらかにデータがない角度では相関値が大幅に下がってしまうためです。

補正ファイルに対し、mrcImageAverageにて平均化を行います。

出力ファイル

xy平面

yz平面

zx平面

最小

最大
平均値
標準偏差

標準誤差

-2.32263 (22, 29, 20)

5.20816 (19, 24, 22)
0.0844992
0.49404

0.00195286

@@ 行456: / 行456: @@
 		</tr>
 	</table>
-<div>-single のときよりもyz平面がはっきりしています。</div>
 <br>

「電子線トモグラフィー」の版間の差分

2014年7月14日 (月) 01:14時点における版

目次

前処理(窓関数)

位置合わせ

mrcImageCorrelationを使用した場合

実行例1

実行例1

実行例2(繰り返し)

mrc2Dto3Dで実行

実行例1

実行例2(２軸傾斜)

実行例3(Double)

ラドン変換を使った３次元再構成で実行

実行例1

実行例2

ミッシングエリア

画像の位置、フォーカスの問題

平行移動の補正

軸の決定

トモグラフに使われる画像処理

平滑化

実行例1

セグメンテーション

３次元画像の切り出し

実行例1

２次元画像の切り出し

実行例1

実行例2(2軸投影)

実行例1

実行例2

案内メニュー

検索